杂题记录

1838. 最高频元素的频数

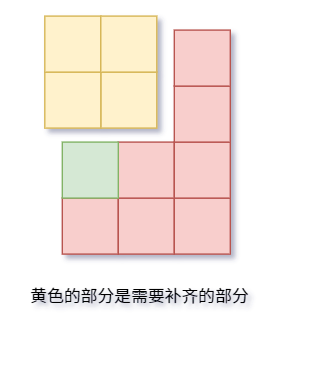
题目的要求是，在给定的元素内，使数组齐平。例如下图是一个 [1，2，4] 的数组，当 k = 5时补齐的状态。所以答案为 3 。

所以可以使用一个滑动窗口，在这个滑动范围之内，都会尝试去用 k 将数组补齐。要使用滑动窗口，必须先让它排个序！此时已经是 (nlogn)了。

由于排序数组了，每次枚举在区间内最大的数，会尝试用 k 去补齐。在滑动循环内只能由两种情况：（假设滑动区间为 left ~ right）

尝试将区间的数向 nums[right] 补齐，使用的次数 sum 小于等于 k。

直接更新当前答案。

// 此刻之前的元素已经与 nums[right - 1] 补齐
// 所以现在只需要把之间的差补齐
nums += (nums[right] - nums[right - 1]) * (right - left);
res = Math.max(res, right - left + 1);

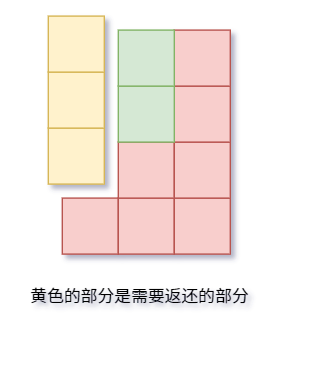
尝试将区间的数向 nums[right] 补齐，使用的次数 sum 大于 k。

这种情况不符合题目题意，需要收缩窗口。

第一步：将 left 向 nums[right] 补齐时所占的次数返回，即 sum - <所占部分>。第二步：将 left + 1。

sum -= nums[right] - nums[left];

完整JavaScript代码：

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number}
 */
var maxFrequency = function(nums, k) {
    nums.sort((a, b) => a - b);
    let res = 1;
    let [left, right, sum] = [0, 1, 0];
    for (; right < nums.length; ++ right) {
        sum += (nums[right] - nums[right-1]) * (right - left);
        while (sum > k) {
            sum -= nums[right] - nums[left];
            left++;
        }
        res = Math.max(res, right - left + 1);
    }
    return res;
};

剑指 Offer 52. 两个链表的第一个公共节点

输入两个链表，找出它们的第一个公共节点。

解题思路和动图均来自：leetcode-腐烂的橘子

我们使用两个指针 node1，node2 分别指向两个链表 headA，headB 的头结点，然后同时分别逐结点遍历。

当 node1 到达链表 headA 的末尾时，重新定位到链表 headB 的头结点；

当 node2 到达链表 headB 的末尾时，重新定位到链表 headA 的头结点；

这样，当它们相遇时，所指向的结点就是第一个公共结点。

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param  {ListNode} headA
 * @param  {ListNode} headB
 * @return {ListNode}
 */
var getIntersectionNode = function(headA, headB) {
    if (headA == null || headB == null) {
        return null;
    }
    
    let [p1, p2] = [headA, headB];
    while (p1 !== p2) {
        p1 = p1 === null ? headB : p1.next;
        p2 = p2 === null ? headA : p2.next;
    }
    return p1;
};

138. 复制带随机指针的链表

思路：

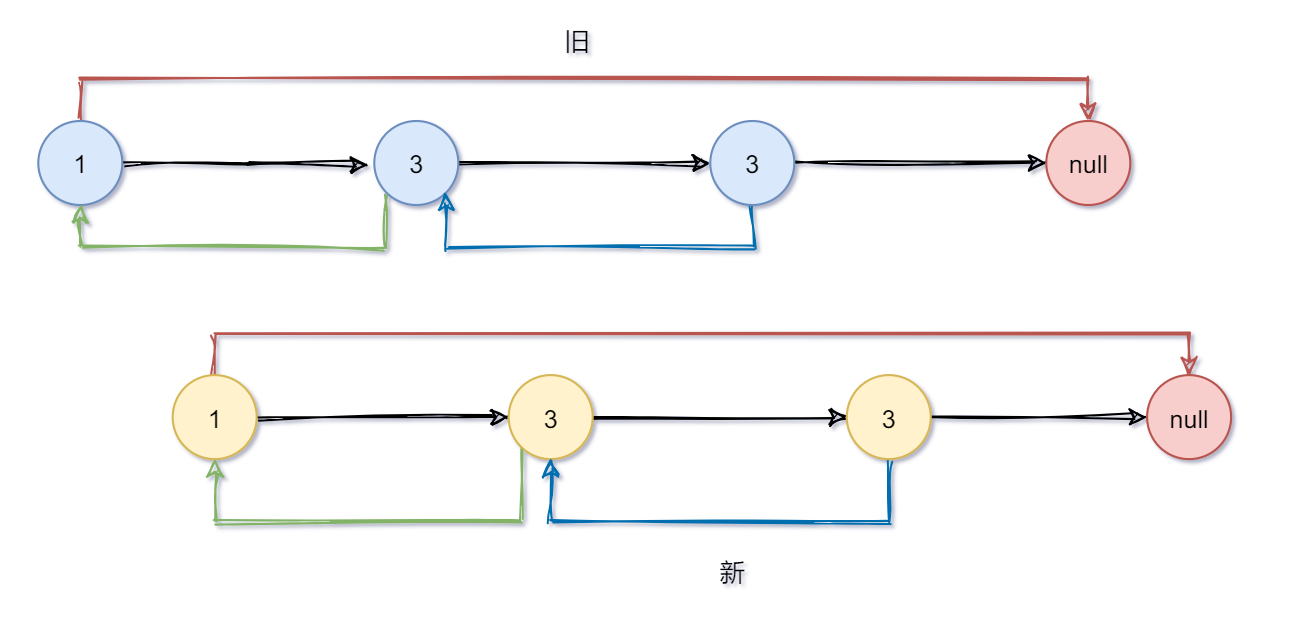
先在原链表上进行复制（蓝色是旧的，黄色是新的）

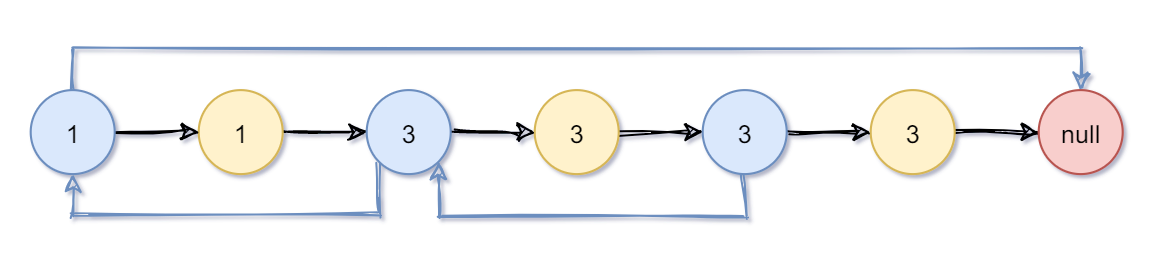
我们先让random指向原链表中的。

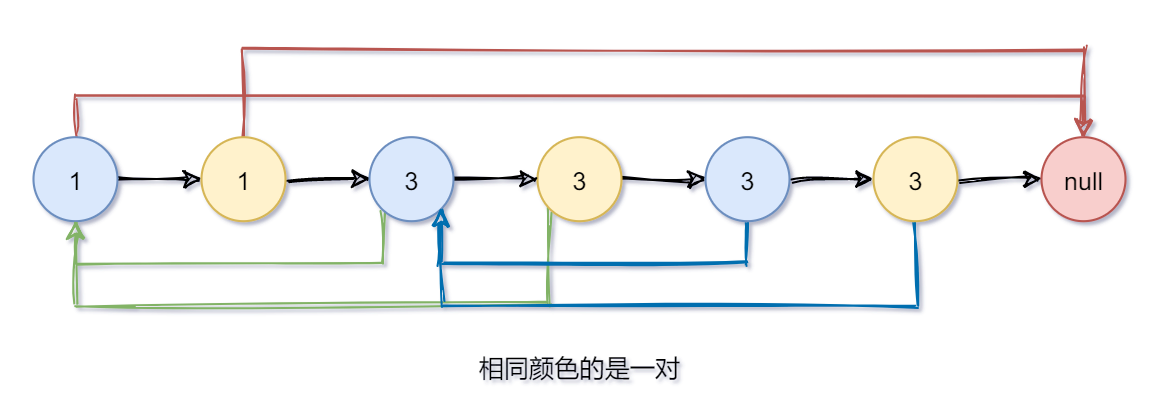
统一让新节点的random指向原链表中的下一个节点，就是random的新节点了。

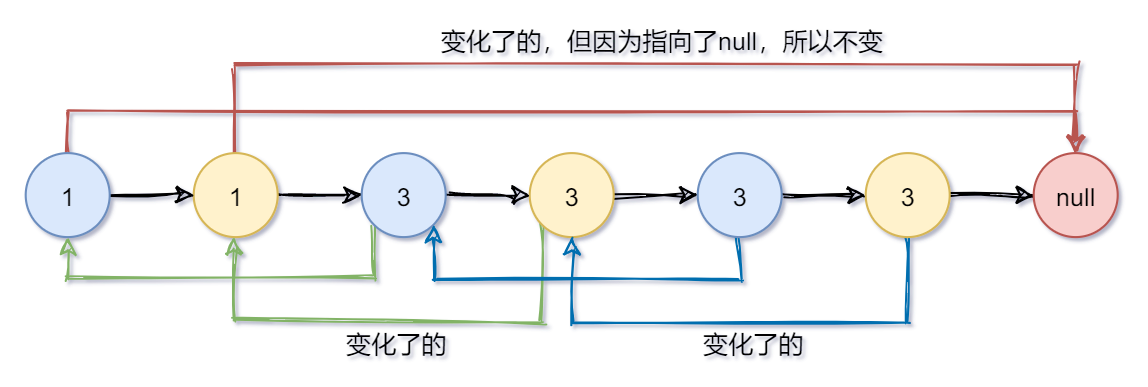
最后再进行分裂

比如 node.next = node.next.next ，就是直接越过一个节点（越过新节点直接指向旧节点）。

/**
 * // Definition for a Node.
 * function Node(val, next, random) {
 *    this.val = val;
 *    this.next = next;
 *    this.random = random;
 * };
 */

/**
 * @param {Node} head
 * @return {Node}
 */
var copyRandomList = function(head) {
    if (head === null) return null;
    // 复制一份
    for (let node = head; node; node = node.next.next) {
        const newNode = new Node(node.val, null, node.random);
        newNode.next = node.next;
        node.next = newNode;
    }
    
    // 复制random链表
    for (let node = head; node; node = node.next.next) {
        const newNode = node.next;
        newNode.random = newNode.random ? newNode.random.next : null;
    }
    
    // 分裂
    // 还原原来的链表、将新链表分离出去
    const res = head.next;
    for (let node = head; node; node = node.next) {
        const newNode = node.next;
        node.next = node.next ? node.next.next : null;
        newNode.next = newNode.next ? newNode.next.next : null;
    }
    return res;
};

1893. 检查是否区域内所有整数都被覆盖

再回忆一下差分。

差分求前缀和 -> 得到原数组
在一段区间内的数组元素都加上一个数 c -> diff[left] += c; diff[right+1] -= c

这道题的 ranges 每个元素给的都是一个区间的 left 和 right，接着把 1 当成上面式子的 c，这样就能把 left 到 right之间的数出现次数 +1了。

下图的 ranges 数组已经给出，diff 是差分数组，prefix 是前缀和数组，它也代表每个元素出现的次数。

index 标红的数字即为满足条件的下标。

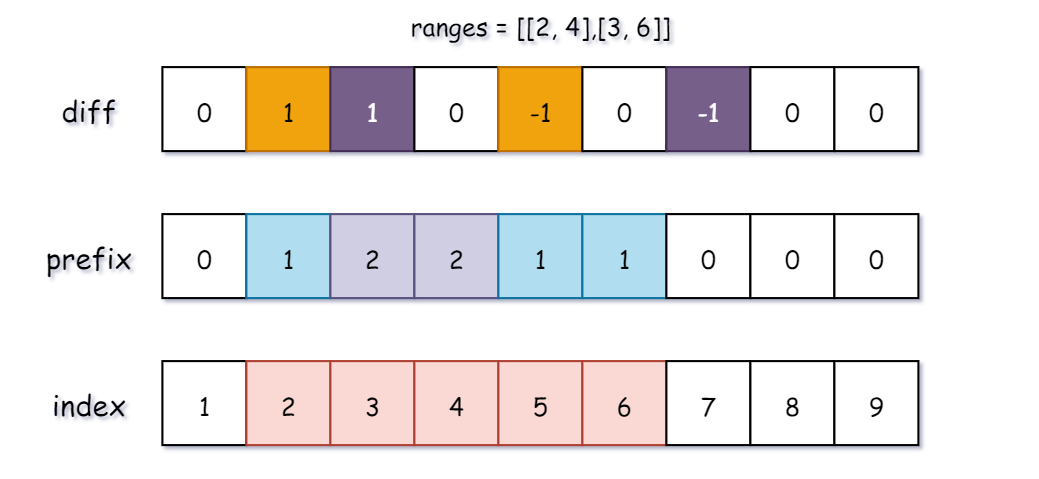
所以思路就是先构造差分数组，通过差分数组去构造前缀和数组，求出每个数组出现的频率。

最后再从 left 遍历到 right，如果都满足就返回 true 就可以了。

/**
 * @param {number[][]} ranges
 * @param {number} left
 * @param {number} right
 * @return {boolean}
 */
var isCovered = function(ranges, left, right) {
    const diff = createZeroArray(60);
    // 构造差分数组
    ranges.forEach(x => {
        diff[x[0]] = diff[x[0]] + 1;
        diff[x[1] + 1] = diff[x[1] + 1] - 1;
    });
    
    // 差分数组求前缀和就是每个数字出现的次数
    const prefix = createZeroArray(60);
    for (let i = 1; i <= 51; ++ i) {
        prefix[i] = diff[i] + prefix[i-1];
    }
    
    for (let i = left; i <= right; ++ i) {
        if (prefix[i] === 0) return false;
    }
    return true;
};

function createZeroArray(size){
    const res = [];
    res.length = size;
    res.fill(0, 0, size);
    return res;
}

剑指 Offer 07. 重建二叉树

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

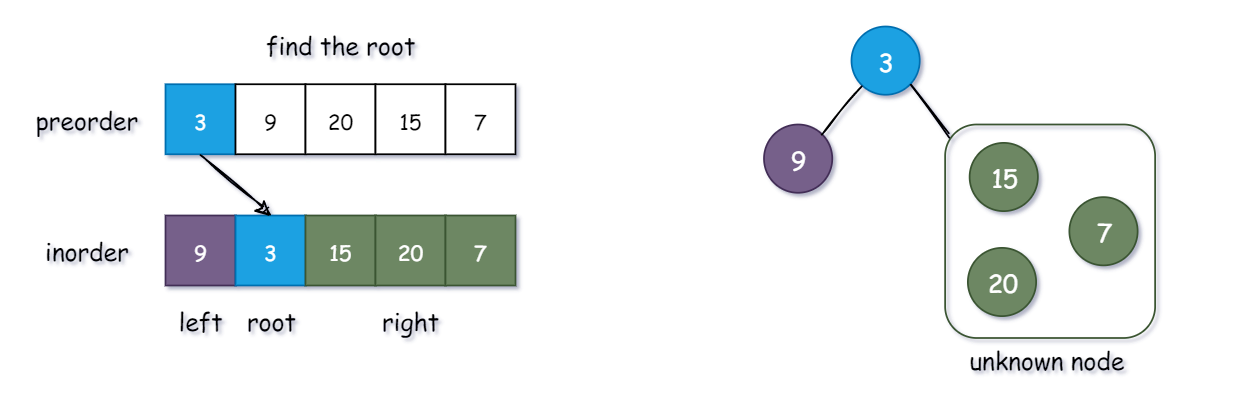
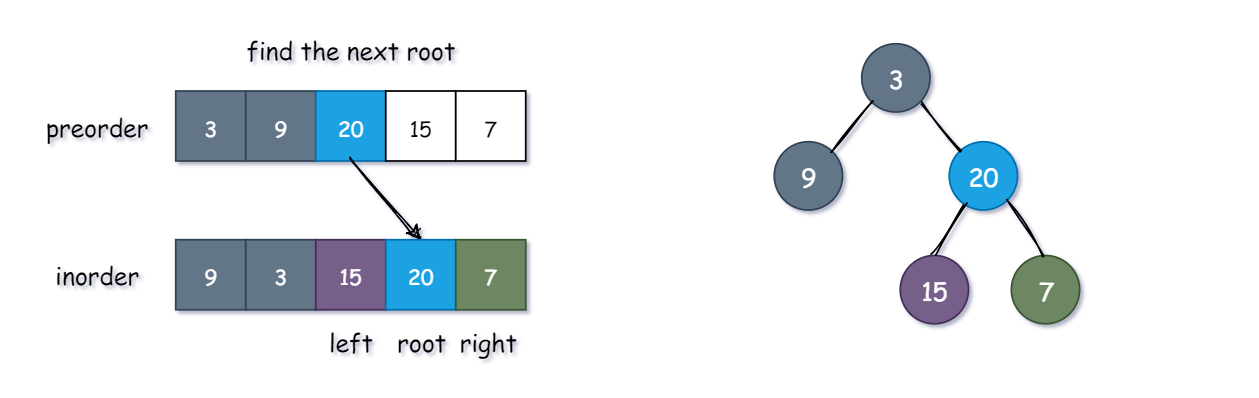
知识点：

前序遍历列表：第一个元素永远是【根节点 (root)】
中序遍历列表：根节点 (root)【左边】的所有元素都在根节点的【左分支】，【右边】的所有元素都在根节点的【右分支】

算法思路：

通过【preorder】确定【根节点 (root)】
将【inorder】的节点分割成【left】和【right】
递归寻找【left】中的【根节点 (left root)】和【right】中的【根节点 (right root)】

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {number[]} preorder
 * @param {number[]} inorder
 * @return {TreeNode}
 */
var buildTree = function (preorder, inorder) {
    if (preorder == 0) return null;
    
    const tree = new TreeNode(preorder[0]);
    
    const divideIdx = inorder.indexOf(tree.val);
    
    const leftPre = preorder.slice(1, divideIdx + 1);
    const leftIn = inorder.slice(0, divideIdx);
    const left = buildTree(leftPre, leftIn);
    
    const rightPre = preorder.slice(divideIdx + 1);
    const rightIn = inorder.slice(divideIdx + 1);
    const right = buildTree(rightPre, rightIn);
    
    tree.left = left, tree.right = right;
    return tree;
};

剑指 Offer 04. 二维数组中的查找

题解来自：leetcode-Krahets

我们将矩阵逆时针旋转 45° ，并将其转化为图形式，发现其类似于二叉搜索树 ，即对于每个元素，其左分支元素更小、右分支元素更大。因此，通过从 “根节点” 开始搜索，遇到比 target 大的元素就向左，反之向右，即可找到目标值 target 。

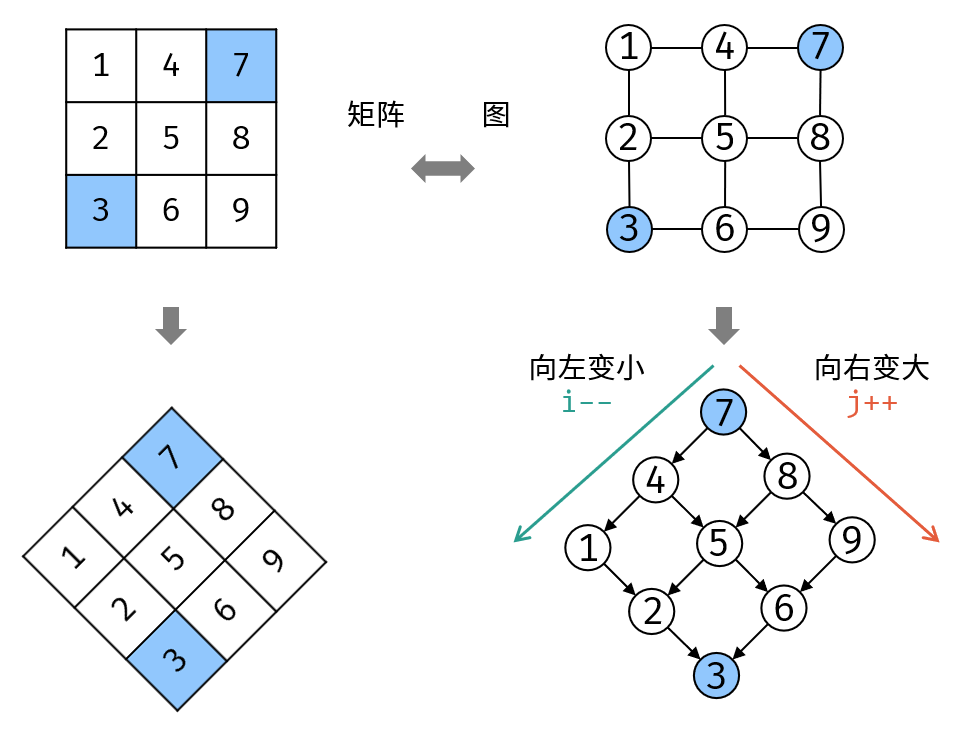
算法流程：

从矩阵 matrix 左下角元素（索引设为 (i, j) ）开始遍历，并与目标值对比：

当 matrix[i][j] > target 时，执行 i-- ，即消去第 i 行元素；
当 matrix[i][j] < target 时，执行 j++ ，即消去第 j 列元素；
当 matrix[i][j] = target 时，返回 true ，代表找到目标值。

若行索引或列索引越界，则代表矩阵中无目标值，返回 false 。

/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {boolean}
 */
var findNumberIn2DArray = function(matrix, target) {
    let [x, y] = [matrix.length - 1, 0];
    while (x >= 0 && y < matrix[0].length) {
        const now = matrix[x][y];
        if (now > target) x--; 
        else if (now < target) y++;
        else return true;
    }
    return false;
};

L1-050 倒数第N个字符串 (15 分)

十进制与二十六进制相互转换

L1-6 福到了 (15 分)

getchar(); // 读取上一行换行符
getline(cin, str); // 读取一行到 string str 中

L2-3 名人堂与代金券 (25 分)

结构体数组排序

struct student {
    string email;
    int score;
    bool operator< (const student &S) const {
        if (score != S.score) return score > S.score; // 成绩降序
        else return email < S.email; // 邮箱升序
    }
}stu[N];

// ......

sort(stu, stu + n);

L2-028 秀恩爱分得快 (25 分)

bool exitsA = find(pic[i].begin(), pic[i].end(), aId) != pic[i].end();

L1-042 日期格式化 (5 分)

整数前补 0

printf("%d-%02d-%02d", y, m, d);

L1-3 阅览室 (20 分)

unordered_map 判断存在和删除

m.count(id); // exist
m.erase(id); // delete

L1-048 矩阵A乘以B (15 分)

1 2 3
4 5 6

8 9 0
2 3 4
6 7 8

res

1 * 7 + 2 * 1 + 3 * 5 | 1 * 8 + 2 * 2 + 3 * 6 | 1 * 9 + 2 * 3 + 3 * 7 | 1 * 0 + 2 * 4 + 3 * 8
4 * 7 + 5 * 1 + 6 * 5 | 4 * 8 + 5 * 2 + 6 * 6 | 4 * 9 + 5 * 3 + 6 * 7 | 4 * 0 + 5 * 4 + 6 * 8

tip

dijkstra 函数式写法

优良题解：分解路径 + 枚举中间节点 + dijkstra

typedef long long LL;
typedef pair<int, int> PII;
#define x first
#define y second
#define N 100010
#define INF 0x3f3f3f3f3f3f3f3f

class Solution {
public:
    LL dist1[N], dist2[N], dist3[N];
    int st[N];
    LL res = INF;
    vector<PII> head[N], back[N];

    void dijkstra(int n, int start, vector<PII> * node, LL * dist) {
        memset(st, 0, sizeof st);
        priority_queue<PII, vector<PII>, greater<PII>> heap;
        dist[start] = 0; 
        st[start] = 1;
        heap.push({0, start});
        while (heap.size()) {
            PII the = heap.top();
            heap.pop();

            int p = the.y;
            int w = the.x;
            if (st[p] == 0) continue;
            st[p] = 0;

            for (int i = 0; i < node[p].size(); ++ i) {
                int nextp = node[p][i].y;
                int nextw = node[p][i].x;

                if (dist[p] + nextw < dist[nextp]) {
                    dist[nextp] = dist[p] + nextw;
                    heap.push({dist[nextp], nextp});
                    st[nextp] = 1;
                }
            }
        }
    }


    long long minimumWeight(int n, vector<vector<int>>& edges, int src1, int src2, int dest) {
        memset(dist1, 0x3f, sizeof dist1);
        memset(dist2, 0x3f, sizeof dist2);
        memset(dist3, 0x3f, sizeof dist3);

        for (int i = 0; i < edges.size(); ++ i) {
            vector<int> the = edges[i];
            int a = the[0], b = the[1], w = the[2];
            head[a].push_back({w, b});
            back[b].push_back({w, a});
        }

        dijkstra(n, src1, head, dist1);
        dijkstra(n, src2, head, dist2);
        dijkstra(n, dest, back, dist3);

        for (int i = 0; i < n; ++ i) {
            if (dist1[i] == INF || dist2[i] == INF || dist3[i] == INF) continue;
            res = min(res, dist1[i] + dist2[i] + dist3[i]);
        }

        return res == INF ? -1 : res;
    }
};

L3-028 森森旅游 (30 分)

tip

和上面那题一样，双向单源最短路

multiset：维护一个有序序列（从小到达） set：如果用它，必须存 PII 以区分相同的元素

#include <bits/stdc++.h>

using namespace std;
typedef long long LL;
typedef pair<LL, int> PII;
#define x first
#define y second

const LL N = 100010, INF = 0x3f3f3f3f3f3f3f3f;

vector<PII> head[N], back[N];
LL dist1[N], dist2[N];
bool st[N];
LL change[N];

int n, m, q;

void dijkstra(int start, vector<PII> * node, LL * dist) {
    memset(st, 0, sizeof st);

    priority_queue<PII, vector<PII>, greater<PII>> heap;
    dist[start] = 0;
    st[start] = 1;
    heap.push({0, start});

    while (heap.size()) {
        PII the = heap.top();
        heap.pop();

        int p = the.y, w = the.x;
        if (st[p] == 0) continue;
        st[p] = 0;

        for (int i = 0; i < node[p].size(); ++ i) {
            int nextp = node[p][i].y, nextw = node[p][i].x;
            if (dist[p] + nextw < dist[nextp]) {
                dist[nextp] = dist[p] + nextw;
                heap.push({dist[nextp], nextp});
                st[nextp] = 1;
            }
        }
    }
}

int main() {
    // freopen("1.txt", "r", stdin);

    memset(dist1, 0x3f, sizeof dist1);
    memset(dist2, 0x3f, sizeof dist2);
    
    cin >> n >> m >> q;
    for (int i = 1; i <= m; ++ i) {
        int a, b, w, t;
        cin >> a >> b >> w >> t;
        head[a].push_back({w, b});
        back[b].push_back({t, a});
    }

    for (int i = 1; i <= n; ++ i) {
        cin >> change[i];
    }

    dijkstra(1, head, dist1);
    dijkstra(n, back, dist2);

    multiset<LL> S;
    for (int i = 1; i <= n; ++ i) {
        if (dist1[i] == INF || dist2[i] == INF) continue;

        S.insert(dist1[i] + dist2[i] / change[i] + (dist2[i] % change[i] ? 1 : 0));
    }

    for (int j = 1; j <= q; ++ j) {
        LL i, newVal; cin >> i >> newVal;
        
        if (dist1[i] != INF && dist2[i] != INF) {
            LL old = dist1[i] + dist2[i] / change[i] + (dist2[i] % change[i] ? 1 : 0);
            S.erase(S.find(old)); // 必须用 find，如果有重复的值，会一起删除

            change[i] = newVal;

            LL newRes = dist1[i] + dist2[i] / change[i] + (dist2[i] % change[i] ? 1 : 0);
            S.insert(newRes);
        }

        cout << *S.begin() << endl;
    }

    return 0;
}

杂题记录

1838. 最高频元素的频数

剑指 Offer 52. 两个链表的第一个公共节点

138. 复制带随机指针的链表

1893. 检查是否区域内所有整数都被覆盖

剑指 Offer 07. 重建二叉树

剑指 Offer 04. 二维数组中的查找

L1-050 倒数第N个字符串 (15 分)

L1-6 福到了 (15 分)

L2-3 名人堂与代金券 (25 分)

L2-028 秀恩爱分得快 (25 分)

L1-042 日期格式化 (5 分)

L1-3 阅览室 (20 分)

L1-048 矩阵A乘以B (15 分)

L2-024 部落 (25 分)

L3-029 还原文件 (30 分)

2203. 得到要求路径的最小带权子图

tip

L3-028 森森旅游 (30 分)

tip